
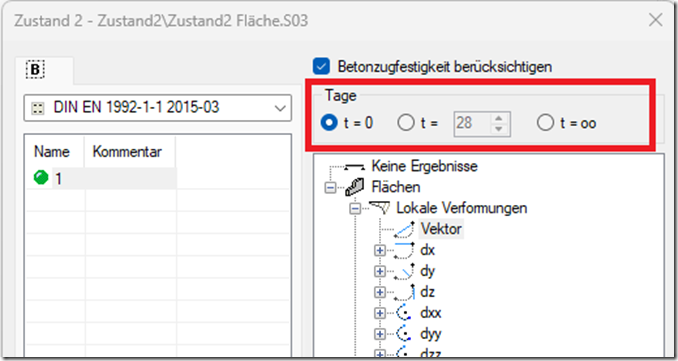
Schwinden wird über eine analoge Temperatureinwirkung berücksichtigt (Zilch, Zehetmaier, 10.4.6.5, „Bemessung im konstruktiven Betonbau“, Springer).Dazu wird zunächst ein Schwindmoment aus einer gleichmäßigen…
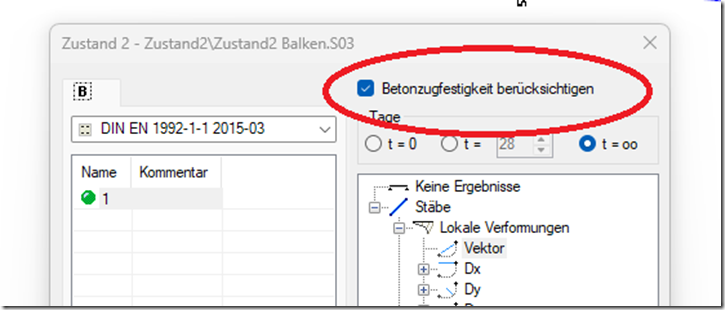
Bei Verformungsnachweisen im Stahlbetonbau wird häufig „im Zustand II“ gerechnet – also mit gerissenen Querschnitten und Beton ausschließlich als Druckwerkstoff. In Wirklichkeit trägt der Beton zwischen den Rissen in der…