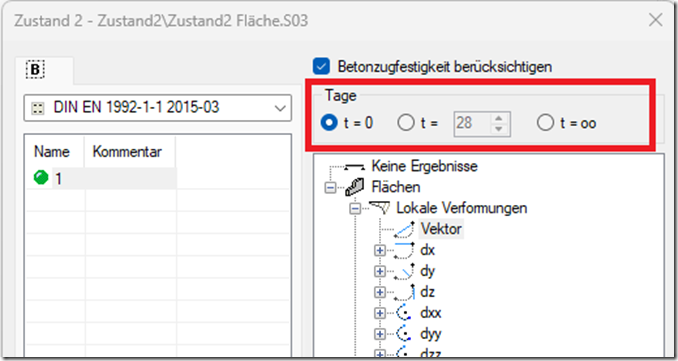
Schwinden wird über eine analoge Temperatureinwirkung berücksichtigt (Zilch, Zehetmaier, 10.4.6.5, „Bemessung im konstruktiven Betonbau“, Springer).
Dazu wird zunächst ein Schwindmoment aus einer gleichmäßigen Schwinddehnung ε_cs im Querschnitt berechnet.
Bezeichnungen:
ε_cs = Schwinddehnung
E_s = E‑Modul des Stahls
A_s0, A_su = vorhandene Bewehrung oben bzw. unten
z_s = Abstand zwischen oberer und unterer Bewehrungslage
Normalkräfte aus behindertem Schwinden in den Bewehrungslagen:
N_cs0 = ε_cs · E_s · A_s0
N_csu = ε_cs · E_s · A_su
Schwindmoment:
M_cs,∞ = z_s · (N_cs0 − N_csu)
Ist die obere und untere Bewehrung identisch, so ist M = 0; liegt die Bewehrung überwiegend nur auf einer Seite, so ist |M| am größten.
Äquivalente Temperaturänderung
Aus diesem Schwindmoment wird eine äquivalente Temperaturänderung ΔT ermittelt, indem das Schwindmoment M einem Temperaturzwangmoment gleichgesetzt wird.
Es gilt:
ΔT = M · h / (E · I · α_T)
wobei
h = Querschnittshöhe
E = verwendetes Elastizitätsmodul (Zustand‑II‑Steifigkeit)
I = maßgebendes Trägheitsmoment
α_T = Wärmeausdehnungskoeffizient
Zeitabhängigkeit des Schwindens
Schwinden ist zeitabhängig; das Schwindmaß wächst mit der Zahl der Tage t und nähert sich einem Endwert an.
Im Programm wird dieser Verlauf über einen Faktor b(t) zwischen 0 und 1 erfasst, der mit der Zeit zunimmt und das Schwindmoment skaliert:
M_cs(t) = b(t) · M_cs,∞
Zur Berechnung von b(t) verwendet das Programm eine glatte, monoton wachsende Funktion in der Form
b(t) = ( t / (t + 500) )^(1/9)
Für t = 0 ist b(0) = 0: direkt nach dem Betonieren wird das Schwinden noch nicht angesetzt.
Für große Zeiten t → ∞ geht der Bruch t / (t + 500) gegen 1, damit nähert sich b(t) dem Wert 1 an, erreicht ihn aber nicht.
Durch die Potenz 1/9 steigt b(t) anfangs spürbar, flacht aber mit zunehmender Zeit ab, sodass der zusätzliche Schwindzuwachs im Bereich vieler Monate und Jahre nur noch gering ist.
Damit wird im Zustand‑II‑Modell sowohl das Niveau als auch die zeitliche Entwicklung des Schwindens in einer einfachen, numerisch gut handhabbaren Form im Programm berücksichtigt.
Hier eine kleine Tabelle mit typischen Werten des Faktors b(t) = ( t / (t + 500) )^(1/9):
| Tage t | Faktor b(t) |
|---|---|
| 0 | 0,000 |
| 1 | 0,417 |
| 10 | 0,647 |
| 28 | 0,722 |
| 56 | 0,775 |
| 100 | 0,819 |
| 500 | 0,926 |
| 1000 | 0,956 |